Calendar correction

In this Chapter

This chapter is divided in two parts. The first one (theory) outlines the rationale for calendar correction and the underlying modelling. The second part (practice) describes how relevant regressors for calendar correction are built in JDemetra+.

As calendar effects are deterministic, they can be corrected with a regression model. In the algorithms X13-ARIMA and TRAMO-SEATS it boils down to adding suitable regressors to the pre-treatment phase). This chapter will describe how to generate a set of regressors corresponding to the desired correction, which will happen according to the following steps:

step 1: generate a calendar (usually national calendar of interest). If this step is skipped a default calendar, not taking into account country-specific holidays will be used.
step 2: generate regressors based on the above defined calendar

Regressors will have the same frequency as the raw data, thus an aggregation process will be defined unless the data is daily.

step 2b: a specific variable for modelling the easter effect (or any other moving holiday effect like ramadan) can also be defined

Most of the functions are designed for quarterly and monthly data. What applies to daily and weekly data will be highlighted.

Regressors are corrected for deterministic seasonality through a long-term mean correction

step 3: these regressors have to be plugged-in in pre-adjustment phase of a seasonal adjustment estimation. How to do this is detailed in chapters on pre-treatment and SA of High-Frenquency data.

How to generate other types of regressors is described here and how to plug them into reg-arima models is detailed here

Rationale for Calendar correction

A calendar is heterogeneous, it at least composed of:

trading days: days usually worked, taking into account the company’s sector. (Most frequently Mondays through Fridays when not bank holidays).
week-ends
bank holidays

For a given year as well as throughout the years, every month doesn’t have the same number of days per day-type, which implies that all months/quarters aren’t “equal”, even for a given type of month or quarter. This causes calendar effects which have to be removed to allow sounder comparisons following the same principle as seasonality correction.

Two types of effects result from this heterogeneity:

length of period (month/quarter) (leap-year or direct correction)
composition of period (type of day)

This second effect is also relevant for daily (and weekly) data.

An additional easter effect can be modelled, as for some series, variations linked to Easter can be seen over a few days prior or following Easter. For example, flowers and chocolate sales might rise significantly as Easter approaches. (in practice this effect is very rare, it is better to deactivate by default detection)

Modelling calendar effects

Regression Model for type of days

For each period \(t\), the days are divided in \(K\) groups \(\lbrace{D_{t1},\dots, D_{tK}\rbrace}\).

The groups of days can be anything (trading days, working days, Sundays + holidays assimilated to Sundays…) ADD

We write \(N_t=\sum_1^K{D_{ti}}\), the number of days of the period \(t\)

Two terms appear:

the specific effect of a type of day \(i\) as a contrast between the number of days \(i\) and the number of Sundays and bank holidays
the effect of the month’s (or period’s) length.

Once seasonally adjusted, this term comes down to the leap year effect:

for all months except Februaries \(\bar{N}_t = N_t\)
for Februaries \(\bar{N}_t=28.25\) and \(N_{t}=28\) or \(N_{t}=29\)

The effect of one day of the group \(i\) is measured by \(\alpha_i\), so that the global effect of the group \(i\) for the period \(t\) is \(\alpha_i D_{ti}\)

The global effect of all the days for the period \(t\) is

\[ \sum_{i=1}^K{\alpha_i D_{ti}} = \bar\alpha N_t + \sum_{i=1}^K{(\alpha_i-\bar\alpha) D_{ti}} \]

where \(\bar\alpha=\sum_{i=1}^K{w_i \alpha_i}\) with \(\sum_{i=1}^Kw_i=1\)

So,

\[ \sum_{i=1}^K{(\alpha_i-\bar\alpha) w_i} = \sum_{i=1}^K{\alpha_iw_i}-\bar\alpha\sum_{i=1}^K w_i=0 \]

LEAP YEAR part to comment

We focus now on \(\sum_{i=1}^K{(\alpha_i-\bar\alpha) D_{ti}}\), the actual trading days effects (excluding the length of period effect).

Writing \(\alpha_i-\bar\alpha = \beta_i\) and using that \(\sum_{i=1}^K{\beta_i w_i} = 0\), we have that

\[ \sum_{i=1}^K{\beta_i D_{ti}}=\sum_{i=1}^K{\beta_i(D_{ti} - \frac{w_i}{w_K}}D_{tK})= \sum_{i=1}^{K-1}{\beta_i(D_{ti} - \frac{w_i}{w_K}}D_{tK}) \]

Note that the relationship is valid for any set of weights \(w_i\). It is also clear that the contrasting group of days can be any group:

\[ \sum_{i=1}^{K-1}{\beta_i(D_{ti} - \frac{w_i}{w_K}}D_{tK}) = \sum_{i=1}^{K, i \neq J}{\beta_i(D_{ti} - \frac{w_i}{w_J}}D_{tJ}) \]

The “missing” coefficient is easily derived from the others:

\[ \beta_K = -\frac{1}{w_K}\sum_{i=1}^{K-1}{\beta_i w_i} \]

Correction for deterministic seasonality

In the case of seasonal adjustment, we further impose that the regression variables don’t contain deterministic seasonality. That is achieved by removing from each type of period (month, quarter…) its long term average. We write \(\bar{D_i^y}\) the long term average of the yearly number of days in the group \(i\) and \(\bar{D_{i,J}^y}\) the long term average of the number of days in the group \(i\) for the periods \(J\) (for instance, average number of Mondays in January…).

The corrected contrast for the time t belonging to the period J is:

\[ C_{ti}=D_{ti}-\bar{D_{i, J}^y}-\frac{w_i}{w_K}(D_{tK}- \bar{D_{K, J}^y}) \]

How is the long term mean computed? Probabilistic approach (more on this soon)

Weights for different groups of days

We can define different sets of weights. The usual one consists in giving the same weight to each type of days. \(w_i\) is just proportional to the number of days in the group \(i\). In the case of “week days”, \(w_0 = \frac{5}{7}\) (weeks) and \(w_1=\frac{2}{7}\) (week-ends). In the case of “trading days”, \(w_i=\frac{1}{7}\) … Another approach consists in using the long term yearly averages, taking into account the actual holidays. We get now that \(w_i=\frac{\bar{D_i^y}}{365.25}\).

After the removal of the deterministic seasonality, the variables computed using the two sets of weights considered above are very similar. In the case of the “trading days”, the difference for the time \(t\), belonging to the period \(J\), and for the day \(i\) with contrast \(K\) is \((1-\frac{w_i}{w_K})(D_{tK}- \bar{D_{K, J}^y})\), which is usually small. By default, JD+ uses the first approach, which is simpler. The second approach is implemented in the algorithmic modules, but not available through the graphical interface.

Use in Reg-ARIMA models

In the context of Reg-ARIMA modelling, we can also observe that the global effect of the trading days doesn’t depend neither on the used weights (we project on the same space) nor on the contrasting group (see above) nor on the long term corrections (removed by differencing).

The estimated coefficients slightly change if we use different weights (not if we use a different contrasting group). It must also be noted that the choices affect the T-Stat of the different coefficients (not the joint F-Test), which can lead to other solutions when those T-Stats are used for selecting the regression variables (Tramo). Considering that the leap year/length of period variable is nearly independent of the other variables, the test on that variable is not very sensitive to the various specifications.

Interpretation

The use of different specifications of the trading days doesn’t impact the final results (except through some automatic selection procedure). It just (slightly) changes the way we interpret the estimated coefficients.

Easter effect

Stock series

Generating Regressors for calendar correction

The following parts details how to build customized regressors for calendar correction using

graphical user interface (GUI)
rjd3toolkit package.

To take specific holidays into account a calendar has to be defined, regressors will be built subsequently.

As regressors have the same data frequency as the input series, several cases:

for daily series : regressors are dummies representing each holidays
for weekly, monthly and quarterly series regressors are aggregated indicators, the way of grouping different types of days and holidays has to be specified.

In GUI

Creating calendars

The customized calendar can be directly linked to the calendar correction option in GUI while specifying a seasonal adjustment process. See chapters on SA or SA of HF data.

Default Calendar

In the graphical user interface, calendars in are stored in the Workspace window in the Utilities section. In the default calendar, country-specific national holidays are not taken into account, it reflects only the usual composition of the weeks in the calendar periods.

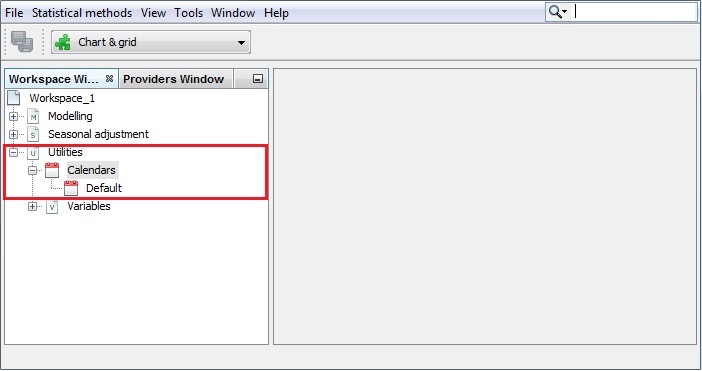
To view the details of the default calendar: double click on it

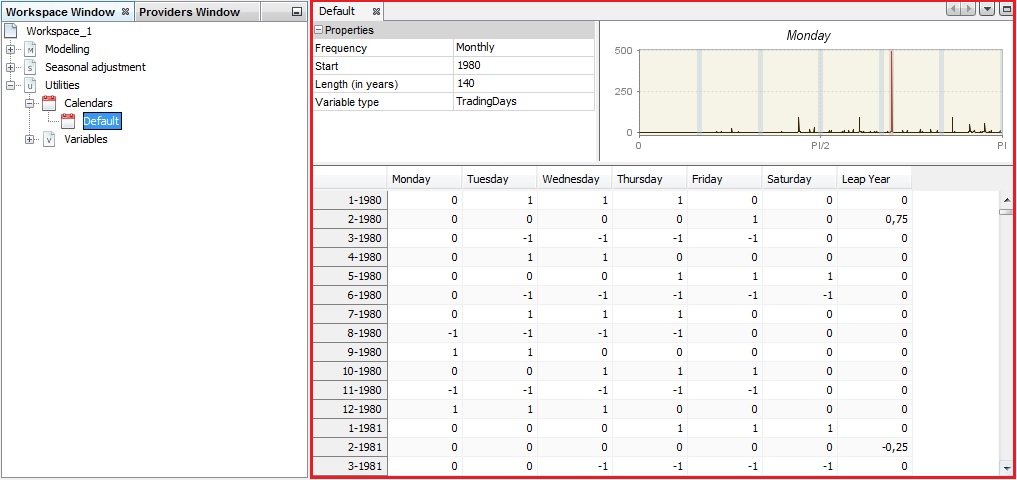
Set Properties

In the Properties panel the user can set:

Frequency (monthly, quarterly..)
Trading days or working days regressors

Trading days: 6 contrast variables

number of Mondays - number of Sundays

and one regressor for the leap year effect.

Working Days: 1 contrast variable (\(number\ of\ working days (monday to friday) - number\ of\ Saturdays and Sundays\),…) and one regressor for the leap year effect.

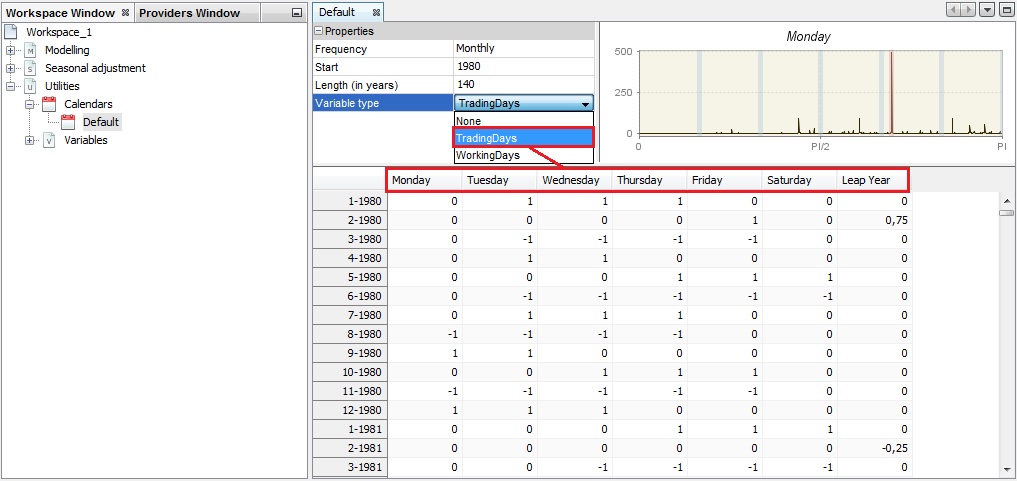
Modification of the initial settings for the Default calendar

Spectrum visualization

The top-right panel displays the spectrum for the given calendar variable. By default, the first variable from the table is shown.

To change it, click on the calendar variable header.

Calendar variables shouldn’t have a peak neither at a zero frequency (trend) nor the seasonal frequencies.

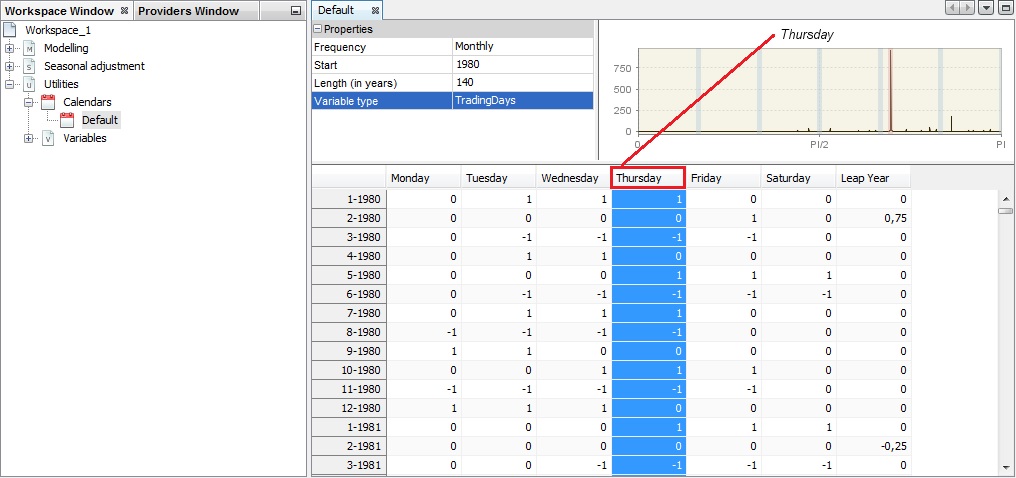
Modify an existing Calendar

click the option Edit from the context menu
the list of holidays defined for this calendar is displayed

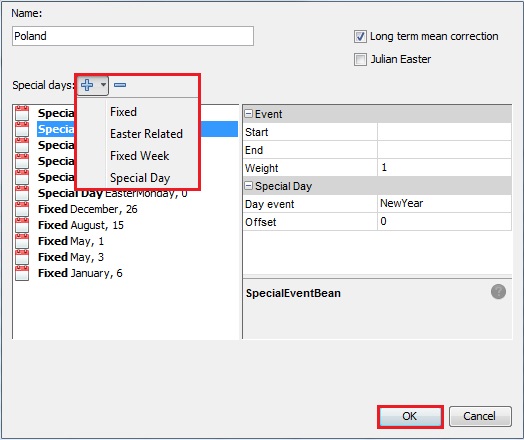
To add a holiday unfold the + menu
To remove a holiday click on it and choose the - button

**Removing a holiday from the calendar**

Creating a new calendar

An appropriate calendar, containing the required national holidays, needs to be created to adjust a series for country-specific calendar effects.

right click on the Calendar item from the Workspace window and choose Add

Three options are available:

National calendars: allows to include country-specific holidays
Composite calendars : creates calendar as a weighted sum of several national calendars
Chained calendars : allows to chain two national calendars before and after a break

National Calendar

To define a national calendar: right click on Calendar item in the Utility panel of the workspace window

To add a holiday unfold the + menu
To remove a holiday from the list click on it and choose the - button.

Four options are available here:

- **Fixed** : holiday occurring at the same date

- **Easter Related**: holiday that depends on Easter Sunday date

- **Fixed Week**: fixed holiday that always falls in a specific week of a given month

- **Special Day**:  choose a holiday from a list of pre-defined holidays (link to table)

to use Julian Easter

To add a holiday from this list to the national calendar, choose the Special day item from the Special days list.

**Adding a pre-defined holiday to the calendar**

By default, when the Special Days option is selected, JDemetra+ always adds Christmas to the list of selected holidays. The user can change this initial choice by specifying the settings in the panel on the right and clicking OK. The settings that can be changed include:

Start: starting date for the holiday (expecting yyyy-mm-dd) Default is the starting date of the calendar (empty cell).
End: same as start
Weight : specifies the impact of the holiday on the series. The default weight is 1 (full weight) assuming that the influence of the holiday is the same as a regular Sunday. If less the a value between 0 and 1 can be assigned.
Day event: a list of pre-defined holidays (link to table)
Offset: allows to set a holiday as related to a pre-specified holiday by specifying the distance in days (e.g Easter Sunday). Default offset is 1. It can be positive or negative. Positive offset: defines a holiday following the pre-specified holiday. Negative offset: defines a holiday preceding the selected pre-specified.

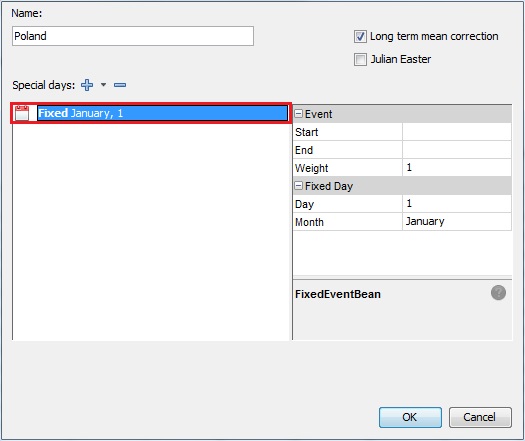
Choosing a pre-defined holiday from the list
To define a fixed holiday not included in the list of pre-defined holidays:
- choose Fixed from the Special days list: by default January, 1 is displayed. Specify the settings:
Start: starting date for the holiday (expecting yyyy-mm-dd) Default is the starting date of the calendar (empty cell).
End: same as start
Weight : specifies the impact of the holiday on the series. The default weight is 1 (full weight) assuming that the influence of the holiday is the same as a regular Sunday. If less the a value between 0 and 1 can be assigned.
Day: day of month when the fixed holiday is celebrated.
Month: month, in which the fixed holiday is celebrated.

Add Corpus Christi: example of an Easter related holiday not included in the special day list(link to table). It is is a moving holiday celebrated 60 days after Easter
- choose the Easter related item from the Special days list.
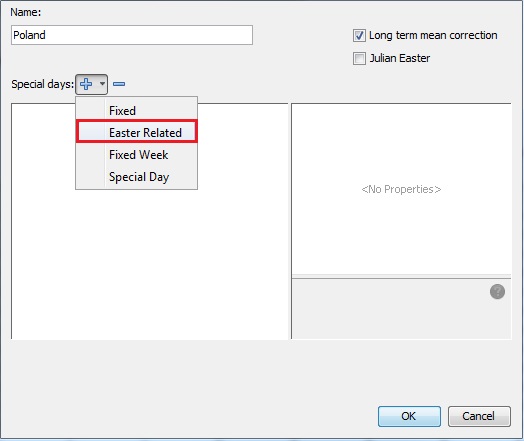By default Easter + 1 is displayed. Setting can be changed :
Start: starting date for the holiday (expecting yyyy-mm-dd) Default is the starting date of the calendar (empty cell).
End: same as start
Weight : specifies the impact of the holiday on the series. The default weight is 1 (full weight) assuming that the influence of the holiday is the same as a regular Sunday. If less the a value between 0 and 1 can be assigned.
Offset: To define Corpus Christi enter 60, as it is celebrated 60 days after Easter Sunday.

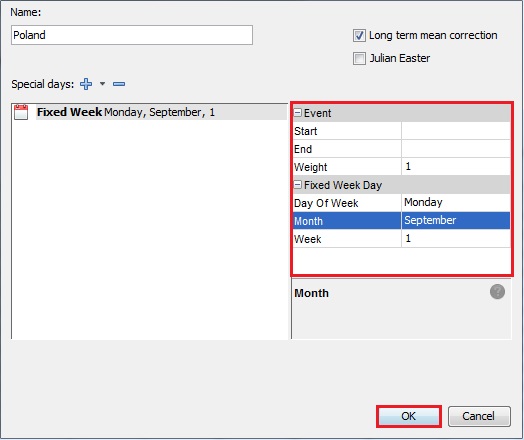
Fixed week option: when dealing with holidays occurring on the same week of a given month. Example: Labour Day in the USA and Canada, celebrated on the first Monday of September in Canada
- choose Fixed Week from the Special days list.
Text

Available settings are:

Start: starting date for the holiday (expecting yyyy-mm-dd) Default is the starting date of the calendar (empty cell).
End: same as start
Weight : specifies the impact of the holiday on the series. The default weight is 1 (full weight) assuming that the influence of the holiday is the same as a regular Sunday. If less the a value between 0 and 1 can be assigned
Day of Week: day of week when the holiday is celebrated each year
Month: month, in which the holiday is celebrated each year
Week: number denoting the place of the week in the month: between 1 and 5

The list of the holidays should contain only unique entries. Otherwise, a warning, as shown in the picture below, will be displayed.

A calendar without a name cannot be saved. Fill the Name box before saving the calendar.

Example : final view of a properly defined calendar for Poland

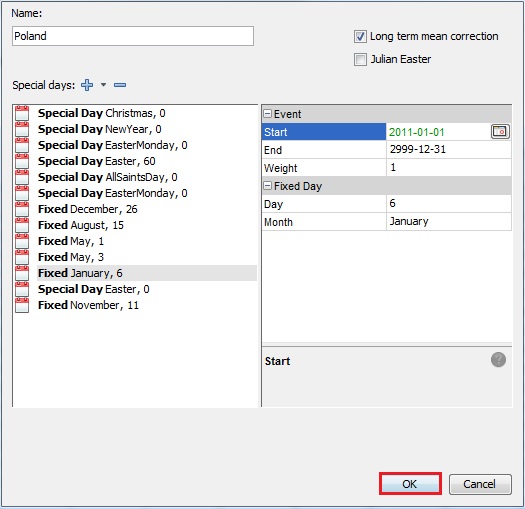
The calendar is visible in the Workspace window

To display the available options right-click on it

A national calendar can be edited, duplicated (to create another calendar) and/or analysed (double click to display it in the panel on the right) or deleted.

Chained Calendar

Creating a chained calendar is relevant when a major break occurs in the definition of the country-specific holidays.

First define the 2 (or \(N\)) national calendars corresponding to each regime as explained in the section above.

To define a chained calendar: right click on Calendar item in the Utility panel of the workspace window

In the Properties panel specify:

first and the second calendar
break date

Composite Calendar

Creating a composite calendar is relevant when correcting series which include data from more than one country/region. This option can be used, for example, to create the calendar for the European Union or to create the national calendar for a country, in which regional holidays are celebrated.

First define the relevant national calendars corresponding to each member state/region as explained above.

To define a chained calendar: right click on Calendar item in the Utility panel of the workspace window

Fill the name box
Mark the regional calendars to be used
Assign a weight to each calendar.

Importing an existing calendar from a file

Right click on the Calendar item from the Workspace window and choose the Import item from the menu.

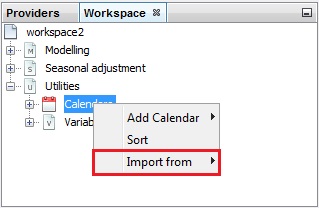
choose the appropriate file and open it

JDemetra+ adds it to the calendars list

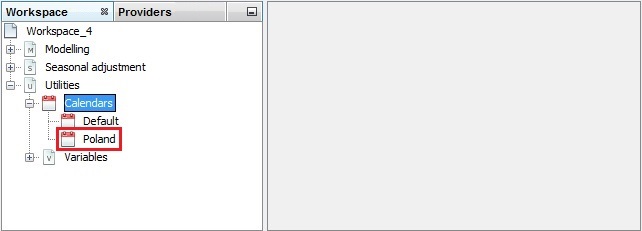
**A list of calendars with a newly imported calendar**

Example of a calendar file

#### Generating regressors

Type of days

Leap year

Length of Period

(adjust param)

Easter

stock TD

In R with rjd3toolkit

Version 3 of JDemetra+ allows to build calendar regressors using the rjd3toolkit package.

The underlying concepts are identical to those available in the graphical user interface (GUI) as described above. R functions replicate the same process and all arguments and outputs are detailed in rjd3toolkit help pages. The sections below provide basic examples.

Note that, RJDemetra package based on version 2 of JDemetra+, doesn’t allow to build calendars and generate regressors. Thus, two approaches are possible when using version 2

use built in regressors (“working days” or “trading days”) not taking into account national holidays
import user defined calendar regressors

Creating calendars

National Calendar

Creating a national calendar with rjd3toolkit.

## French calendar
frenchCalendar <- national_calendar(days = list(
    fixed_day(7, 14), # Bastille Day
    fixed_day(5, 8, validity = list(start = "1982-05-08")), # End of 2nd WW
    special_day("NEWYEAR"),
    special_day("CHRISTMAS"),
    special_day("MAYDAY"),
    special_day("EASTERMONDAY"),
    special_day("ASCENSION"), #
    special_day("WHITMONDAY"),
    special_day("ASSUMPTION"),
    special_day("ALLSAINTSDAY"),
    special_day("ARMISTICE")
))

Holidays can be created with the following ways:

as fixed days (falling on the exact same date every year)

day <- fixed_day(
    month = 12,
    day = 25,
    weight = .9,
    validity = list(start = "1968-02-01", end = "2010-01-01")
)
day # December 25th, with weight=0.9, from February 1968 until January 2010

as special days, when on the list of common holidays, which is available in the function’s halp page.

# Get the list
?special_day
# To define a holiday for the day after Christmas, with validity and weight
special_day("CHRISTMAS",
    offset = 1, weight = 0.8,
    validity = list(start = "2000-01-01", end = "2020-12-01")
)

as a fixed week day

fixed_week_day(7, 2, 3) # second Wednesday of July

as an easter related holiday

easter_day(1) # Easter Monday
easter_day(-2) # Good Friday

An example of calendar bringing together all options

MyCalendar <- national_calendar(list(
    fixed_day(7, 21),
    special_day("NEWYEAR"),
    special_day("CHRISTMAS"),
    fixed_week_day(7, 2, 3), # second Wednesday of July
    special_day("MAYDAY"),
    easter_day(1), # Easter Monday
    easter_day(-2), # Good Friday
    fixed_day(5, 8, validity = list(start = "1982-05-08")), # End of 2nd WW
    single_day("2001-09-11"), # appearing once
    special_day("ASCENSION"),
    easter_day( # Corpus Christi
        offset = 60,
        julian = FALSE,
        weight = 0.5,
        validity = list(start = "2000-01-01", end = "2020-12-01")
    ),
    special_day("WHITMONDAY"),
    special_day("ASSUMPTION"),
    special_day("ALLSAINTSDAY"),
    special_day("ARMISTICE")
))

For any defined calendar, it is possible to retrieve the long term-mean correction values which would be applied on a given set of regressors.

### Long-term means of a calendar
BE <- national_calendar(list(
    fixed_day(7, 21),
    special_day("NEWYEAR"),
    special_day("CHRISTMAS"),
    special_day("MAYDAY"),
    special_day("EASTERMONDAY"),
    special_day("ASCENSION"),
    special_day("WHITMONDAY"),
    special_day("ASSUMPTION"),
    special_day("ALLSAINTSDAY"),
    special_day("ARMISTICE")
))
class(BE)
lt <- long_term_mean(BE, 12,
    groups = c(1, 1, 1, 1, 1, 0, 0),
    holiday = 7
)

Chained Calendar

Creating a chained calendar is relevant when a major break occurs in the definition of the country-specific holidays.

First define the 2 (or \(N\)) national calendars corresponding to each regime as explained in the section above.

Belgium <- national_calendar(list(special_day("NEWYEAR"), fixed_day(7, 21)))
France <- national_calendar(list(special_day("NEWYEAR"), fixed_day(7, 14)))
chained_cal <- chained_calendar(France, Belgium, "2000-01-01")

Composite Calendar

Belgium <- national_calendar(list(special_day("NEWYEAR"), fixed_day(7, 21)))
France <- national_calendar(list(special_day("NEWYEAR"), fixed_day(7, 14)))
composite_calendar <- weighted_calendar(list(France, Belgium), weights = c(1, 2))

Generating regressors

First for monthly, Q, bi monthly…(set this right)

Type of days

This section describes how to generate regressors to correct for type of days effects. They can be based on a default calendar (no specific holidays taken into account) or on a customized calendar.

Trading day regressors without holidays using rjd3toolkit::td function

# Monthly regressors for Trading Days: each type of day is different
# contrasts to Sundays (6 series)
?td
regs_td <- td(frequency = 12, c(2020, 1), 60, groups = c(1, 2, 3, 4, 5, 6, 0), contrasts = TRUE)

The groups argument allows to build groups of days, as daus belonging to the same group will be identified by the same number, and to set a reference for contrasts with the number 0.

Trading day regressors with pre-defined holidays using rjd3toolkit::calendar_td function

The rjd3toolkit::calendar_td function

?calendar_td
# first define a calendar
BE <- national_calendar(list(
    fixed_day(7, 21),
    special_day("NEWYEAR"),
    special_day("CHRISTMAS"),
    special_day("MAYDAY"),
    special_day("EASTERMONDAY"),
    special_day("ASCENSION"),
    special_day("WHITMONDAY"),
    special_day("ASSUMPTION"),
    special_day("ALLSAINTSDAY"),
    special_day("ARMISTICE")
))
# generate regressors
calendar_td(BE,
    frequency = 12, c(1980, 1), 240, holiday = 7, groups = c(1, 1, 1, 2, 2, 3, 0),
    contrasts = FALSE
)
# here three groups and one reference are defined
# Mondays = Tuesdays= Wednesdays (`1`)
# Thursdays= Fridays (`2`)
# Saturdays (`3`)
# Sundays and all holidays (`0`)

Leap year

Length of Period

adjust param

Easter Regressor

Create a regressor for modelling the easter effect:

# Monthly regressor, five-year long, duration 8 days, effect finishing on Easter Monday
ee <- easter_variable(frequency = 12, c(2020, 1), length = 5 * 12, duration = 8, endpos = 1)

Display Easter Sunday dates in given period

The function below allows to display the date of Easter Sunday for each year, in the defined period. Dates are displayed in “YYYY-MM-DD” format and as a number of days since January 1st 1970.

# Dates from 2018(included) to 2023 (included)
easter_dates(2018, 2023)

stock TD

Daily data (dummies)

## dummies corresponding to holidays
q <- holidays(BE, "2020-01-01", 365.25, type = "All")
tail(q)

Weekly data

Test for Residual Calendar effects

(To be added: where exactly to find the tests in GUI and R)

We consider below tests on the seasonally adjusted series (\(sa_t\)) or on the irregular component (\(irr_t\)). When the reasoning applies on both components, we will use \(y_t\). The functions \(stdev\) stands for “standard deviation” and \(rms\) for “root mean squares”

The tests are computed on the log-transformed components in the case of multiplicative decomposition.

TD are the usual contrasts of trading days, 6 variables (no specific calendar).

Non significant irregular

When \(irr_t\) is not significant, we don’t compute the test on it, to avoid irrelevant results. We consider that \(irr_t\) is significant if \(stdev( irr_t)>0.01\) (multiplicative case) or if \(stdev(irr_t)/rms(sa_t) >0.01\) (additive case).

F test

The test is the usual joint F-test on the TD coefficients, computed on the following models:

Autoregressive model (AR modelling option)

We compute by OLS:

\[ y_t=\mu + \alpha y_{t-1} + \beta TD_t + \epsilon_t \]

Difference model

We compute by OLS:

\[ \Delta y_t - \overline{\Delta y_t}=\beta TD_t + \epsilon_t \]

So, the latter model is a restriction of the first one (\(\alpha =1, \mu =μ=\overline{\Delta y_t}\))

The tests are the usual joint F-tests on \(\beta \quad (H_0:\beta=0)\).

By default, we compute the tests on the 8 last years of the components, so that they might highlight moving calendar effects.

Remark:

In Tramo, a similar test is computed on the residuals of the Arima model. More exactly, the F-test is computed on \(e_t=\beta TD_t + \epsilon_t\), where \(e_t\) are the one-step-ahead forecast errors.